Last modified: Jan 31 2026 at 10:09 PM • 12 mins read
Getting your Matrix Dimensions Right
Table of contents
- Introduction
- Example Network Architecture
- Dimensions for a Single Training Example
- Bias Vector Dimensions
- Gradient Dimensions (Backpropagation)
- Activation and Z Dimensions
- Vectorized Implementation Dimensions
- Complete Dimension Summary
- Practical Dimension Checking
- Common Dimension Errors
- Debugging Strategy
- Why This Matters
- Key Takeaways
Introduction
When implementing a deep neural network, one of the most effective debugging tools is to systematically check matrix dimensions. Working through dimensions on paper can help you catch bugs before they cause runtime errors.
Pro Tip: Keep a piece of paper handy when coding neural networks. Sketching out matrix dimensions is one of the best ways to verify your implementation!
This lesson shows you how to verify dimensions are consistent throughout your network, building on the forward propagation concepts from the previous lesson.
Example Network Architecture
Let’s work with a concrete example - a 5-layer network:
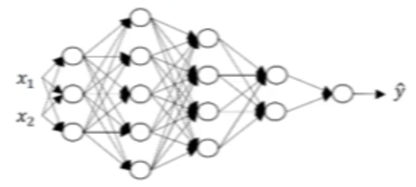
Network specifications:
- $L = 5$ (five layers, not counting input layer)
- 4 hidden layers + 1 output layer
- Input features: $n^{[0]} = n_x = 2$
- Layer sizes: $n^{[1]} = 3$, $n^{[2]} = 5$, $n^{[3]} = 4$, $n^{[4]} = 2$, $n^{[5]} = 1$
Layer Size Summary
| Layer | Type | Number of Units ($n^{[l]}$) |
|---|---|---|
| 0 | Input | $n^{[0]} = 2$ |
| 1 | Hidden | $n^{[1]} = 3$ |
| 2 | Hidden | $n^{[2]} = 5$ |
| 3 | Hidden | $n^{[3]} = 4$ |
| 4 | Hidden | $n^{[4]} = 2$ |
| 5 | Output | $n^{[5]} = 1$ |
Note: So far we’ve only seen networks with a single output unit ($n^{[L]} = 1$), but later courses will cover multi-output networks!
Dimensions for a Single Training Example
Forward Propagation: Layer 1
Let’s start with the forward propagation equation:
\[z^{[1]} = W^{[1]} x + b^{[1]}\]Step 1: Determine output dimension ($z^{[1]}$)
$z^{[1]}$ contains activations for all units in layer 1:
\[z^{[1]}: (n^{[1]}, 1) = (3, 1)\]Step 2: Determine input dimension ($x$)
We have 2 input features:
\[x: (n^{[0]}, 1) = (2, 1)\]Step 3: Solve for $W^{[1]}$ dimension
We need: $(3, 1) = W^{[1]} \times (2, 1)$
By matrix multiplication rules:
\[W^{[1]}: (3, 2)\]Why? A $(3, 2)$ matrix times a $(2, 1)$ vector gives a $(3, 1)$ vector!
General formula:
\[\boxed{W^{[1]}: (n^{[1]}, n^{[0]})}\]Weight Matrix Dimensions: General Rule
For any layer $l$:
\[z^{[l]} = W^{[l]} a^{[l-1]} + b^{[l]}\]Dimension requirement:
\[\boxed{W^{[l]}: (n^{[l]}, n^{[l-1]})}\]Interpretation:
- Rows: Number of units in current layer ($n^{[l]}$)
- Columns: Number of units in previous layer ($n^{[l-1]}$)
Complete Example: All Weight Matrices
Let’s verify dimensions for our 5-layer network:
Layer 1: $z^{[1]} = W^{[1]} a^{[0]} + b^{[1]}$
\[W^{[1]}: (n^{[1]}, n^{[0]}) = (3, 2)\]Layer 2: $z^{[2]} = W^{[2]} a^{[1]} + b^{[2]}$
Need: $(5, 1) = W^{[2]} \times (3, 1)$
\[W^{[2]}: (n^{[2]}, n^{[1]}) = (5, 3)\]Layer 3: $z^{[3]} = W^{[3]} a^{[2]} + b^{[3]}$
\[W^{[3]}: (n^{[3]}, n^{[2]}) = (4, 5)\]Layer 4: $z^{[4]} = W^{[4]} a^{[3]} + b^{[4]}$
\[W^{[4]}: (n^{[4]}, n^{[3]}) = (2, 4)\]Layer 5: $z^{[5]} = W^{[5]} a^{[4]} + b^{[5]}$
\[W^{[5]}: (n^{[5]}, n^{[4]}) = (1, 2)\]Weight Matrix Dimension Table
| Layer $l$ | $W^{[l]}$ Shape | Calculation |
|---|---|---|
| 1 | $(3, 2)$ | $(n^{[1]}, n^{[0]})$ |
| 2 | $(5, 3)$ | $(n^{[2]}, n^{[1]})$ |
| 3 | $(4, 5)$ | $(n^{[3]}, n^{[2]})$ |
| 4 | $(2, 4)$ | $(n^{[4]}, n^{[3]})$ |
| 5 | $(1, 2)$ | $(n^{[5]}, n^{[4]})$ |
Pattern: Each weight matrix connects two adjacent layers!
Bias Vector Dimensions
Bias Vector: Layer 1
From the equation:
\[z^{[1]} = W^{[1]} x + b^{[1]}\]We have:
\[(3, 1) = (3, 2) \times (2, 1) + b^{[1]}\]For addition to work, $b^{[1]}$ must have the same shape as $z^{[1]}$:
\[\boxed{b^{[1]}: (n^{[1]}, 1) = (3, 1)}\]General Rule for Bias Vectors
For any layer $l$:
\[\boxed{b^{[l]}: (n^{[l]}, 1)}\]Interpretation: Bias vector has one element per unit in the layer.
Complete Bias Vector Table
| Layer $l$ | $b^{[l]}$ Shape | Calculation |
|---|---|---|
| 1 | $(3, 1)$ | $n^{[1]} \times 1$ |
| 2 | $(5, 1)$ | $n^{[2]} \times 1$ |
| 3 | $(4, 1)$ | $n^{[3]} \times 1$ |
| 4 | $(2, 1)$ | $n^{[4]} \times 1$ |
| 5 | $(1, 1)$ | $n^{[5]} \times 1$ |
Gradient Dimensions (Backpropagation)
When implementing backpropagation, gradients must match parameter dimensions:
\[\boxed{\begin{align} dW^{[l]} &: \text{same shape as } W^{[l]} = (n^{[l]}, n^{[l-1]}) \\ db^{[l]} &: \text{same shape as } b^{[l]} = (n^{[l]}, 1) \end{align}}\]Why? During gradient descent, we update:
\[W^{[l]} := W^{[l]} - \alpha \, dW^{[l]}\] \[b^{[l]} := b^{[l]} - \alpha \, db^{[l]}\]Subtraction requires matching dimensions!
Activation and Z Dimensions
Single Example Dimensions
For a single training example:
\[z^{[l]} = W^{[l]} a^{[l-1]} + b^{[l]}\] \[a^{[l]} = g^{[l]}(z^{[l]})\]Since activation functions apply element-wise:
\[\boxed{\begin{align} z^{[l]} &: (n^{[l]}, 1) \\ a^{[l]} &: (n^{[l]}, 1) \quad \text{(same as } z^{[l]} \text{)} \end{align}}\]Summary: Single Example Dimensions
| Quantity | Dimension | Description |
|---|---|---|
| $x = a^{[0]}$ | $(n^{[0]}, 1)$ | Input features |
| $W^{[l]}$ | $(n^{[l]}, n^{[l-1]})$ | Weight matrix for layer $l$ |
| $b^{[l]}$ | $(n^{[l]}, 1)$ | Bias vector for layer $l$ |
| $z^{[l]}$ | $(n^{[l]}, 1)$ | Linear output for layer $l$ |
| $a^{[l]}$ | $(n^{[l]}, 1)$ | Activation for layer $l$ |
| $dW^{[l]}$ | $(n^{[l]}, n^{[l-1]})$ | Gradient of $W^{[l]}$ |
| $db^{[l]}$ | $(n^{[l]}, 1)$ | Gradient of $b^{[l]}$ |
Vectorized Implementation Dimensions
Processing Multiple Examples
When implementing vectorization to process $m$ training examples simultaneously, dimensions change!
Single Example (Recap)
\[z^{[1]} = W^{[1]} x + b^{[1]}\]Dimensions:
- $W^{[1]}$: $(n^{[1]}, n^{[0]})$
- $x$: $(n^{[0]}, 1)$
- $b^{[1]}$: $(n^{[1]}, 1)$
- $z^{[1]}$: $(n^{[1]}, 1)$
Vectorized (All Examples)
\[Z^{[1]} = W^{[1]} X + b^{[1]}\]Key change: Stack all examples as columns!
Matrix $X$ (input data):
\[X = \begin{bmatrix} | & | & & | \\ x^{(1)} & x^{(2)} & \cdots & x^{(m)} \\ | & | & & | \end{bmatrix}\] \[X = A^{[0]}: (n^{[0]}, m)\]Matrix $Z^{[1]}$ (linear outputs):
\[Z^{[1]} = \begin{bmatrix} | & | & & | \\ z^{[1](1)} & z^{[1](2)} & \cdots & z^{[1](m)} \\ | & | & & | \end{bmatrix}\] \[Z^{[1]}: (n^{[1]}, m)\]Dimension Verification
Let’s check: $(n^{[1]}, m) = (n^{[1]}, n^{[0]}) \times (n^{[0]}, m) + (n^{[1]}, 1)$
\[(n^{[1]}, m) = (n^{[1]}, m) + (n^{[1]}, 1)\]Broadcasting: $b^{[1]}$ with shape $(n^{[1]}, 1)$ is broadcast to $(n^{[1]}, m)$ and added element-wise!
Python Broadcasting Explanation
# W shape: (n[1], n[0])
# X shape: (n[0], m)
# b shape: (n[1], 1)
Z = np.dot(W, X) + b
# Step 1: Matrix multiplication
# np.dot(W, X) -> (n[1], m)
# Step 2: Broadcasting
# b (n[1], 1) is broadcast to (n[1], m)
# Each column gets the same bias vector
# Step 3: Addition
# (n[1], m) + (n[1], m) -> (n[1], m)
Vectorized Dimensions: General Rule
For any layer $l$:
\[\boxed{\begin{align} W^{[l]} &: (n^{[l]}, n^{[l-1]}) \quad \text{(unchanged)} \\ b^{[l]} &: (n^{[l]}, 1) \quad \text{(unchanged)} \\ Z^{[l]} &: (n^{[l]}, m) \quad \text{(added } m \text{ dimension)} \\ A^{[l]} &: (n^{[l]}, m) \quad \text{(added } m \text{ dimension)} \end{align}}\]Special case: $A^{[0]} = X$ has shape $(n^{[0]}, m)$
Comparison: Single vs Vectorized
| Quantity | Single Example | Vectorized ($m$ examples) |
|---|---|---|
| Input | $x: (n^{[0]}, 1)$ | $X: (n^{[0]}, m)$ |
| Weights | $W^{[l]}: (n^{[l]}, n^{[l-1]})$ | $W^{[l]}: (n^{[l]}, n^{[l-1]})$ ✓ Same |
| Biases | $b^{[l]}: (n^{[l]}, 1)$ | $b^{[l]}: (n^{[l]}, 1)$ ✓ Same |
| Linear output | $z^{[l]}: (n^{[l]}, 1)$ | $Z^{[l]}: (n^{[l]}, m)$ |
| Activations | $a^{[l]}: (n^{[l]}, 1)$ | $A^{[l]}: (n^{[l]}, m)$ |
| Weight gradient | $dw^{[l]}: (n^{[l]}, n^{[l-1]})$ | $dW^{[l]}: (n^{[l]}, n^{[l-1]})$ ✓ Same |
| Bias gradient | $db^{[l]}: (n^{[l]}, 1)$ | $db^{[l]}: (n^{[l]}, 1)$ ✓ Same |
| Z gradient | $dz^{[l]}: (n^{[l]}, 1)$ | $dZ^{[l]}: (n^{[l]}, m)$ |
| A gradient | $da^{[l]}: (n^{[l]}, 1)$ | $dA^{[l]}: (n^{[l]}, m)$ |
Key insight: Parameters ($W, b$) and their gradients ($dW, db$) have the same dimensions in both cases!
Complete Dimension Summary
Parameters (Single + Vectorized)
| Parameter | Dimension | Notes |
|---|---|---|
| $W^{[l]}$ | $(n^{[l]}, n^{[l-1]})$ | Same for single and vectorized |
| $b^{[l]}$ | $(n^{[l]}, 1)$ | Same for single and vectorized |
| $dW^{[l]}$ | $(n^{[l]}, n^{[l-1]})$ | Same as $W^{[l]}$ |
| $db^{[l]}$ | $(n^{[l]}, 1)$ | Same as $b^{[l]}$ |
Activations and Intermediate Values
Single example (lowercase):
| Variable | Dimension |
|---|---|
| $x = a^{[0]}$ | $(n^{[0]}, 1)$ |
| $z^{[l]}$ | $(n^{[l]}, 1)$ |
| $a^{[l]}$ | $(n^{[l]}, 1)$ |
| $dz^{[l]}$ | $(n^{[l]}, 1)$ |
| $da^{[l]}$ | $(n^{[l]}, 1)$ |
Vectorized (uppercase):
| Variable | Dimension |
|---|---|
| $X = A^{[0]}$ | $(n^{[0]}, m)$ |
| $Z^{[l]}$ | $(n^{[l]}, m)$ |
| $A^{[l]}$ | $(n^{[l]}, m)$ |
| $dZ^{[l]}$ | $(n^{[l]}, m)$ |
| $dA^{[l]}$ | $(n^{[l]}, m)$ |
Practical Dimension Checking
Step-by-Step Verification Process
When debugging your implementation:
1. Write down the equation
\[Z^{[l]} = W^{[l]} A^{[l-1]} + b^{[l]}\]2. List known dimensions
- $A^{[l-1]}$: $(n^{[l-1]}, m)$ (previous layer activation)
- $Z^{[l]}$: $(n^{[l]}, m)$ (desired output)
3. Solve for unknown dimensions
- $W^{[l]}$ must be: $(n^{[l]}, n^{[l-1]})$
- $b^{[l]}$ must be: $(n^{[l]}, 1)$ (broadcasts to $(n^{[l]}, m)$)
4. Verify matrix multiplication
\((n^{[l]}, n^{[l-1]}) \times (n^{[l-1]}, m) = (n^{[l]}, m)\) ✓
Python Dimension Checking Code
def check_dimensions(W, b, A_prev, layer):
"""
Verify dimensions for layer l forward propagation
Args:
W: weight matrix for layer l
b: bias vector for layer l
A_prev: activations from layer l-1
layer: layer number (for printing)
"""
n_l, n_l_minus_1 = W.shape
m = A_prev.shape[1]
print(f"Layer {layer} dimension check:")
print(f" W^[{layer}] shape: {W.shape} (expected: ({n_l}, {n_l_minus_1}))")
print(f" b^[{layer}] shape: {b.shape} (expected: ({n_l}, 1))")
print(f" A^[{layer-1}] shape: {A_prev.shape} (expected: ({n_l_minus_1}, {m}))")
# Compute Z
Z = np.dot(W, A_prev) + b
print(f" Z^[{layer}] shape: {Z.shape} (expected: ({n_l}, {m}))")
# Verify
assert W.shape == (n_l, n_l_minus_1), f"W dimension mismatch!"
assert b.shape == (n_l, 1), f"b dimension mismatch!"
assert A_prev.shape[0] == n_l_minus_1, f"A_prev dimension mismatch!"
assert Z.shape == (n_l, m), f"Z dimension mismatch!"
print(" ✓ All dimensions correct!\n")
return Z
Using Assertions in Code
def forward_propagation_one_layer(A_prev, W, b, activation):
"""
Forward propagation for one layer with dimension checks
"""
# Expected dimensions
n_l, n_l_minus_1 = W.shape
m = A_prev.shape[1]
# Dimension assertions (help catch bugs early!)
assert W.shape[1] == A_prev.shape[0], \
f"W columns ({W.shape[1]}) must match A_prev rows ({A_prev.shape[0]})"
assert b.shape == (W.shape[0], 1), \
f"b shape must be ({W.shape[0]}, 1), got {b.shape}"
# Forward propagation
Z = np.dot(W, A_prev) + b
# Verify output dimension
assert Z.shape == (n_l, m), \
f"Z shape should be ({n_l}, {m}), got {Z.shape}"
if activation == "relu":
A = relu(Z)
elif activation == "sigmoid":
A = sigmoid(Z)
# A should have same shape as Z
assert A.shape == Z.shape
cache = (Z, A_prev, W, b)
return A, cache
Common Dimension Errors
Error 1: Wrong Weight Matrix Shape
❌ Mistake: $W^{[l]}$ is $(n^{[l-1]}, n^{[l]})$ instead of $(n^{[l]}, n^{[l-1]})$
# WRONG: Rows = previous layer, Columns = current layer
W1 = np.random.randn(2, 3) # (n[0], n[1])
Z1 = np.dot(W1, X) # ERROR: Can't multiply (2, 3) × (2, m)
✓ Correct: $W^{[l]}$ is $(n^{[l]}, n^{[l-1]})$
# CORRECT: Rows = current layer, Columns = previous layer
W1 = np.random.randn(3, 2) # (n[1], n[0])
Z1 = np.dot(W1, X) # OK: (3, 2) × (2, m) = (3, m)
Error 2: Transposed Input
❌ Mistake: Input $X$ is $(m, n^{[0]})$ instead of $(n^{[0]}, m)$
# WRONG: Examples as rows
X = np.random.randn(100, 2) # (m, n[0])
Z1 = np.dot(W1, X) # ERROR: (3, 2) × (100, 2) = dimension mismatch
✓ Correct: Input $X$ is $(n^{[0]}, m)$
# CORRECT: Examples as columns
X = np.random.randn(2, 100) # (n[0], m)
Z1 = np.dot(W1, X) # OK: (3, 2) × (2, 100) = (3, 100)
Error 3: Bias Shape Mismatch
❌ Mistake: $b^{[l]}$ is $(1, n^{[l]})$ instead of $(n^{[l]}, 1)$
# WRONG: Row vector
b1 = np.random.randn(1, 3) # (1, n[1])
Z1 = np.dot(W1, X) + b1 # Broadcasting error or wrong shape
✓ Correct: $b^{[l]}$ is $(n^{[l]}, 1)$
# CORRECT: Column vector
b1 = np.random.randn(3, 1) # (n[1], 1)
Z1 = np.dot(W1, X) + b1 # OK: broadcasts (3, 1) to (3, m)
Error 4: Gradient Dimension Mismatch
❌ Mistake: $dW^{[l]}$ doesn’t match $W^{[l]}$ shape
# If W1 is (3, 2)
dW1 = np.random.randn(2, 3) # WRONG: (2, 3)
W1 = W1 - alpha * dW1 # ERROR: Can't subtract (3, 2) - (2, 3)
✓ Correct: $dW^{[l]}$ has same shape as $W^{[l]}$
# If W1 is (3, 2)
dW1 = np.random.randn(3, 2) # CORRECT: (3, 2)
W1 = W1 - alpha * dW1 # OK: (3, 2) - (3, 2)
Debugging Strategy
The Paper-and-Pencil Method
When you encounter dimension errors:
Step 1: Write down ALL dimensions
Network: n[0]=2, n[1]=3, n[2]=5, m=100
Layer 1:
W1: (?, ?)
X: (2, 100)
b1: (?, ?)
Z1: (?, ?)
Step 2: Use matrix multiplication rules
Z1 = W1 × X + b1
(?, ?) = (?, ?) × (2, 100) + (?, ?)
We want Z1 to be (3, 100)
So: (3, 100) = (3, 2) × (2, 100) + (3, 1)
Step 3: Verify the pattern holds for all layers
Step 4: Compare with your code
print("W1 shape:", W1.shape) # Should be (3, 2)
print("X shape:", X.shape) # Should be (2, 100)
print("b1 shape:", b1.shape) # Should be (3, 1)
print("Z1 shape:", Z1.shape) # Should be (3, 100)
Dimension Checking Checklist
- $W^{[l]}$ is $(n^{[l]}, n^{[l-1]})$ for all layers
- $b^{[l]}$ is $(n^{[l]}, 1)$ for all layers
- $X$ (input) is $(n^{[0]}, m)$
- $Z^{[l]}$ and $A^{[l]}$ are $(n^{[l]}, m)$ for all layers
- $dW^{[l]}$ matches $W^{[l]}$ shape for all layers
- $db^{[l]}$ matches $b^{[l]}$ shape for all layers
- Matrix multiplications are compatible: $(a, b) \times (b, c) = (a, c)$
- Final output $A^{[L]}$ or $\hat{Y}$ is $(n^{[L]}, m)$
Why This Matters
Bug Prevention
Checking dimensions systematically helps you:
- Catch bugs early: Before runtime errors occur
- Understand the code: Dimensions reveal the data flow
- Debug faster: Narrow down where the error occurred
- Build confidence: Verify your implementation is correct
Andrew Ng’s tip: “When I’m trying to debug my own code, I’ll often pull out a piece of paper and just think carefully through the dimensions of the matrices I’m working with.”
Dimension Consistency = Correct Implementation
If all your dimensions are consistent throughout forward and backward propagation, you’ve eliminated a major class of bugs!
Key Takeaways
- Weight matrix: $W^{[l]}$ has shape $(n^{[l]}, n^{[l-1]})$ - rows = current layer, columns = previous layer
- Bias vector: $b^{[l]}$ has shape $(n^{[l]}, 1)$ - one bias per unit
- Single example: $z^{[l]}, a^{[l]}$ have shape $(n^{[l]}, 1)$
- Vectorized: $Z^{[l]}, A^{[l]}$ have shape $(n^{[l]}, m)$ - add $m$ dimension for training examples
- Parameters unchanged: $W^{[l]}, b^{[l]}$ have same dimensions in single and vectorized implementations
- Gradient shapes match: $dW^{[l]}$ matches $W^{[l]}$, $db^{[l]}$ matches $b^{[l]}$
- Input data: $X = A^{[0]}$ has shape $(n^{[0]}, m)$ - features as rows, examples as columns
- Output predictions: $\hat{Y} = A^{[L]}$ has shape $(n^{[L]}, m)$
- Broadcasting: $b^{[l]}$ shape $(n^{[l]}, 1)$ broadcasts to $(n^{[l]}, m)$ when added to $Z^{[l]}$
- Matrix multiplication rule: $(a, b) \times (b, c) = (a, c)$ - inner dimensions must match
- Element-wise operations: $z^{[l]}$ and $a^{[l]}$ have same dimensions (activation is element-wise)
- Dimension checking tool: Pull out paper and verify dimensions to catch bugs early
- Common mistake: Transposing weight matrices or input data
- Debugging strategy: Print all shapes, verify matrix multiplication compatibility
- Consistency check: If dimensions are consistent throughout, you’ve eliminated major bugs!