Last modified: Jan 31 2026 at 10:09 PM • 5 mins read

Vectorizing Across Multiple Examples

Table of contents

  1. Introduction
  2. Review: Single Example Forward Propagation
  3. The Problem: Multiple Examples
  4. Non-Vectorized Implementation (Slow)
  5. Vectorized Implementation (Fast)
  6. Implementation
  7. Understanding Matrix Dimensions
  8. How to Think About Matrix Layout
  9. Comparison: For-Loop vs Vectorized
  10. Why This Works
  11. Key Takeaways

Introduction

In the previous lesson, we learned how to compute predictions for a single training example. Now we’ll vectorize across multiple training examples to process the entire dataset simultaneously - similar to what we did for logistic regression.

By stacking training examples as columns in a matrix, we can transform our 4 equations with minimal changes to compute outputs for all examples at once.

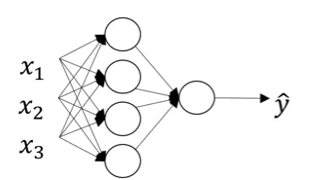
A neural network diagram showing forward propagation with three input features x1, x2, x3 on the left feeding into a hidden layer with four nodes (represented as circles), which then connects to a single output node producing y-hat. The connections between layers are shown with multiple crossing lines indicating full connectivity between each input and hidden node, and between each hidden node and the output. One hidden node is filled in black while others are white, and the output node is also filled in black, suggesting these are the active computation path being illustrated.

Review: Single Example Forward Propagation

For a single training example $x$, we computed:

\[z^{[1]} = W^{[1]} x + b^{[1]}\] \[a^{[1]} = \sigma(z^{[1]})\] \[z^{[2]} = W^{[2]} a^{[1]} + b^{[2]}\] \[a^{[2]} = \sigma(z^{[2]}) = \hat{y}\]

The Problem: Multiple Examples

With $m$ training examples, we need predictions for each:

\[x^{(1)} \rightarrow \hat{y}^{(1)} = a^{[2](1)}\] \[x^{(2)} \rightarrow \hat{y}^{(2)} = a^{[2](2)}\] \[\vdots\] \[x^{(m)} \rightarrow \hat{y}^{(m)} = a^{[2](m)}\]

Notation Clarification

\[a^{[l](i)}\]
  • Square brackets $[l]$: layer number
  • Round brackets $(i)$: training example number

So $a^{2}$ means “activation from layer 2 for training example 3”.

Non-Vectorized Implementation (Slow)

The naive approach uses a for-loop:

for i in range(m):
    # Hidden layer
    z[1](i) = W[1] @ x(i) + b[1]
    a[1](i) = sigmoid(z[1](i))
    
    # Output layer
    z[2](i) = W[2] @ a[1](i) + b[2]
    a[2](i) = sigmoid(z[2](i))

Problem: Processing one example at a time is inefficient. Let’s vectorize!

Vectorized Implementation (Fast)

Step 1: Stack Training Examples as Columns

Create the input matrix $X$ by stacking examples horizontally:

\[X = \begin{bmatrix} | & | & & | \\ x^{(1)} & x^{(2)} & \cdots & x^{(m)} \\ | & | & & | \end{bmatrix}\]

Shape: $(n_x, m)$ where $n_x$ = number of features, $m$ = number of examples

Step 2: Use Capital Letter Matrices

Replace lowercase vectors with uppercase matrices:

Single example notation:

\[x, \quad z^{[1]}, \quad a^{[1]}, \quad z^{[2]}, \quad a^{[2]}\]

Multiple examples notation (stacked as columns):

\[X = [x^{(1)} \ x^{(2)} \ \cdots \ x^{(m)}], \quad \text{shape: } (n_x, m)\] \[Z^{[1]} = [z^{[1](1)} \ z^{[1](2)} \ \cdots \ z^{[1](m)}], \quad \text{shape: } (n^{[1]}, m)\] \[A^{[1]} = [a^{[1](1)} \ a^{[1](2)} \ \cdots \ a^{[1](m)}], \quad \text{shape: } (n^{[1]}, m)\] \[Z^{[2]} = [z^{[2](1)} \ z^{[2](2)} \ \cdots \ z^{[2](m)}], \quad \text{shape: } (n^{[2]}, m)\] \[A^{[2]} = [a^{[2](1)} \ a^{[2](2)} \ \cdots \ a^{[2](m)}], \quad \text{shape: } (n^{[2]}, m)\]

Step 3: Vectorized Forward Propagation

Simply replace lowercase with uppercase:

\[Z^{[1]} = W^{[1]} X + b^{[1]}\] \[A^{[1]} = \sigma(Z^{[1]})\] \[Z^{[2]} = W^{[2]} A^{[1]} + b^{[2]}\] \[A^{[2]} = \sigma(Z^{[2]})\]

That’s it! The same 4 equations, just with capital letters.

Implementation

# Vectorized forward propagation for m examples
# Hidden layer
Z1 = np.dot(W1, X) + b1      # Shape: (4, m)
A1 = sigmoid(Z1)              # Shape: (4, m)

# Output layer
Z2 = np.dot(W2, A1) + b2     # Shape: (1, m)
A2 = sigmoid(Z2)              # Shape: (1, m)

# A2 contains predictions for all m examples
y_hat = A2

Understanding Matrix Dimensions

Let’s verify with $n_x = 3$ features, $n^{[1]} = 4$ hidden units, and $m = 100$ examples:

ComputationDimensionsResult
$W^{[1]} X$$(4 \times 3) \cdot (3 \times 100)$$(4 \times 100)$
$Z^{[1]} = W^{[1]} X + b^{[1]}$$(4 \times 100) + (4 \times 1)$$(4 \times 100)$
$A^{[1]} = \sigma(Z^{[1]})$$\sigma((4 \times 100))$$(4 \times 100)$
$W^{[2]} A^{[1]}$$(1 \times 4) \cdot (4 \times 100)$$(1 \times 100)$
$Z^{[2]} = W^{[2]} A^{[1]} + b^{[2]}$$(1 \times 100) + (1 \times 1)$$(1 \times 100)$
$A^{[2]} = \sigma(Z^{[2]})$$\sigma((1 \times 100))$$(1 \times 100)$

Note: Broadcasting automatically handles adding $b^{[1]}$ (shape $(4,1)$) to each column of the $(4, 100)$ matrix.

How to Think About Matrix Layout

Horizontal Axis: Training Examples

Moving left to right across columns = scanning through training examples.

Vertical Axis: Nodes/Features

Moving top to bottom down rows = scanning through nodes (or features).

Example: Matrix $A^{[1]}$ with 4 Hidden Units and 5 Examples

\[A^{[1]} = \begin{bmatrix} a^{[1](1)}_1 & a^{[1](2)}_1 & a^{[1](3)}_1 & a^{[1](4)}_1 & a^{[1](5)}_1 \\ a^{[1](1)}_2 & a^{[1](2)}_2 & a^{[1](3)}_2 & a^{[1](4)}_2 & a^{[1](5)}_2 \\ a^{[1](1)}_3 & a^{[1](2)}_3 & a^{[1](3)}_3 & a^{[1](4)}_3 & a^{[1](5)}_3 \\ a^{[1](1)}_4 & a^{[1](2)}_4 & a^{[1](3)}_4 & a^{[1](4)}_4 & a^{[1](5)}_4 \end{bmatrix}\]

Interpretation:

  • Top-left $a^{1}_1$: Activation of hidden unit 1 on example 1
  • Moving down: Hidden unit 2, 3, 4 on example 1
  • Moving right: Hidden unit 1 on examples 2, 3, 4, 5
  • Bottom-right $a^{1}_4$: Activation of hidden unit 4 on example 5

Same Pattern for All Matrices

MatrixRows (vertical)Columns (horizontal)
$X$Input features ($x_1, x_2, \ldots, x_{n_x}$)Training examples
$Z^{[1]}, A^{[1]}$Hidden units (nodes 1, 2, 3, 4)Training examples
$Z^{[2]}, A^{[2]}$Output unitsTraining examples

Comparison: For-Loop vs Vectorized

Non-Vectorized (Slow)

# Process one example at a time
for i in range(m):
    z1_i = np.dot(W1, x_i) + b1
    a1_i = sigmoid(z1_i)
    z2_i = np.dot(W2, a1_i) + b2
    a2_i = sigmoid(z2_i)

Time: $O(m)$ iterations

Vectorized (Fast)

# Process all examples simultaneously
Z1 = np.dot(W1, X) + b1
A1 = sigmoid(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = sigmoid(Z2)

Time: $O(1)$ operation (parallelized)

Why This Works

The vectorization works because matrix multiplication naturally implements the “loop” over training examples:

\[W^{[1]} X = W^{[1]} \begin{bmatrix} x^{(1)} & x^{(2)} & \cdots & x^{(m)} \end{bmatrix} = \begin{bmatrix} W^{[1]} x^{(1)} & W^{[1]} x^{(2)} & \cdots & W^{[1]} x^{(m)} \end{bmatrix}\]

Each column of the result corresponds to processing one training example - exactly what the for-loop did, but computed in parallel!

Key Takeaways

  1. Stack training examples as columns to create matrices $X$, $Z^{[l]}$, $A^{[l]}$
  2. Replace lowercase with uppercase: $x \rightarrow X$, $z^{[l]} \rightarrow Z^{[l]}$, $a^{[l]} \rightarrow A^{[l]}$
  3. Same 4 equations work for both single and multiple examples (just change case)
  4. Matrix dimensions: $(n^{[l]}, m)$ where $n^{[l]}$ = units in layer $l$, $m$ = examples
  5. Horizontal (columns): Different training examples
  6. Vertical (rows): Different nodes/features in the layer
  7. Broadcasting handles adding bias vectors to matrices automatically
  8. Vectorization eliminates for-loops and leverages parallel computation