Last modified: Jan 31 2026 at 10:09 PM • 3 mins read

What is a Neural Network?

Table of contents

  1. Introduction
  2. Binary Classification Problem
  3. Image Representation in Computers
  4. Notation for Training Data
  5. Matrix Representation
  6. Key Convention

Introduction

This week covers essential neural network implementation techniques:

  • Vectorization: Processing entire training sets without explicit for loops
  • Forward and Backward Propagation: How computations are organized in neural networks
  • Logistic Regression: Used as a foundation to understand these concepts

Binary Classification Problem

Logistic regression is an algorithm for binary classification. Let’s understand this through an example:

Example Task: Classify whether an image contains a cat or not

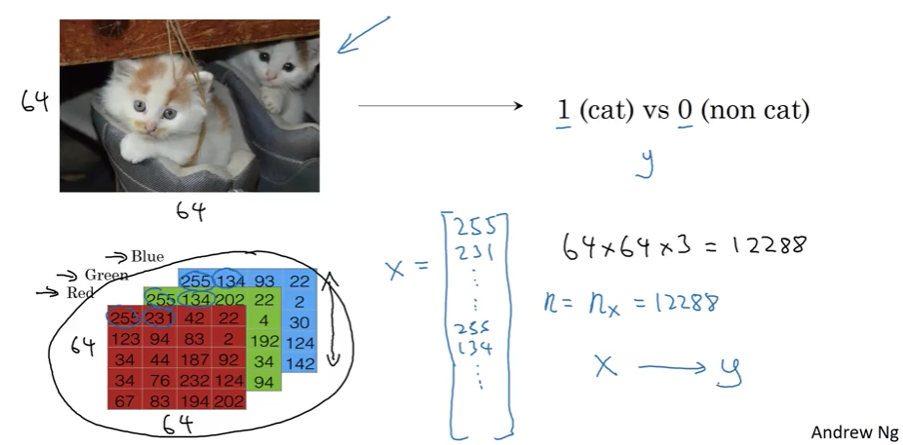
Binary classification example showing two cats in a basket (64x64 pixels) labeled as y=1 for cat versus 0 for non-cat. Below, a diagram illustrates how the 64x64x3 RGB image is unrolled into a feature vector X containing pixel values from red, green, and blue channels (255, 134, 93, 22 for blue; 255, 134, 202, 22 for green; 250, 231, 42, 22 for red), resulting in nx = 64×64×3 = 12288 total features that form the input vector for classification. Created by Andrew Ng

  • Output: y = 1 (cat) or y = 0 (not a cat)

Image Representation in Computers

RGB Color Channels

An image is stored as three separate matrices representing:

  • Red channel
  • Green channel
  • Blue channel

For a 64×64 pixel image:

  • Each channel: 64×64 matrix
  • Total: 3 matrices of pixel intensity values

Converting Images to Feature Vectors

To use an image as input to a neural network, we unroll the pixel values into a feature vector $x$:

Process:

  1. List all red pixel values: [255, 231, ..., ]
  2. List all green pixel values: [255, 134, ..., ]
  3. List all blue pixel values: [...]
  4. Concatenate into one long vector

Dimension Calculation: \(n_x = 64 \times 64 \times 3 = 12,288\)

Where:

  • $n_x$ = dimension of input feature vector
  • Sometimes abbreviated as $n$

Goal: Learn a classifier that takes this feature vector $x$ and predicts label $y$ (1 or 0).

Notation for Training Data

Single Training Example

A single training example is a pair: $(x, y)$

  • $x$: $n_x$-dimensional feature vector
  • $y$: label (0 or 1)

Training Set Notation

Training set with $m$ examples: \((x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), \ldots, (x^{(m)}, y^{(m)})\)

Where:

  • $m$ = number of training examples (sometimes written as $m_{train}$)
  • $m_{test}$ = number of test examples

Matrix Representation

Input Matrix $X$

Stack all training examples as columns in a matrix:

\[X = [x^{(1)} \mid x^{(2)} \mid \cdots \mid x^{(m)}]\]

Dimensions: $X$ is an $n_x \times m$ matrix

  • Rows: $n_x$ (feature dimension)
  • Columns: $m$ (number of examples)

Python notation: X.shape = (nx, m)

Why column-wise?

  • Makes neural network implementation easier
  • Different from some conventions that stack examples as rows

Output Matrix $Y$

Similarly, stack all labels as columns:

\[Y = [y^{(1)} \mid y^{(2)} \mid \cdots \mid y^{(m)}]\]

Dimensions: $Y$ is a $1 \times m$ matrix

Python notation: Y.shape = (1, m)

Key Convention

Throughout this course:

  • Data from different training examples are stacked in different columns
  • Applies to inputs ($x$), outputs ($y$), and other quantities
  • This convention simplifies neural network implementation