Last modified: Jan 31 2026 at 10:09 PM • 4 mins read

Gradient Descent

Table of contents

  1. Introduction
  2. Recap: Logistic Regression Setup
  3. Computation Graph (Forward Pass)
  4. Backward Propagation (Computing Derivatives)
  5. Summary of Derivatives for One Example
  6. Gradient Descent Update (One Example)
  7. Generalizing to $n$ Features
  8. The Big Picture
  9. What About Multiple Training Examples?
  10. Key Takeaways

Introduction

In this lesson, we’ll learn how to compute derivatives to implement gradient descent for logistic regression.

Goal: Understand the key equations needed to implement gradient descent.

Method: We’ll use a computation graph to visualize the process. While this might seem like overkill for logistic regression, it’s excellent preparation for understanding neural networks.

Recap: Logistic Regression Setup

For a single training example:

Prediction: \(\hat{y} = a = \sigma(z)\)

where: \(z = w^T x + b\)

Loss function: \(\mathcal{L}(a, y) = -[y \log(a) + (1-y) \log(1-a)]\)

Where:

  • $a$ = output of logistic regression (same as $\hat{y}$)
  • $y$ = true label

Objective: Modify parameters $w$ and $b$ to reduce the loss.

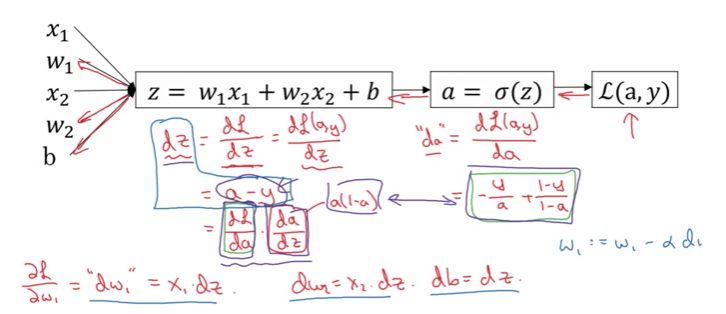
Computation graph diagram showing forward and backward propagation for logistic regression with two features. The forward pass flows left to right: inputs x1 and x2 with weights w1 and w2 plus bias b combine to compute z equals w1x1 plus w2x2 plus b, which feeds into activation a equals sigma of z, then into loss function L of a comma y. Below the main flow are handwritten derivative calculations in red and blue showing backward propagation: dL/dz equals negative dL/da times da/dz with intermediate steps showing a minus y; dw1 equals x1 times dz; dw2 equals x2 times dz; and db equals dz. A small box shows the gradient calculation with values y over a plus 1 minus y over 1 minus a. The diagram illustrates how gradients flow backwards through the network to update parameters w1, w2, and b.

Computation Graph (Forward Pass)

Let’s visualize this for a simple example with 2 features: $x_1$ and $x_2$.

Inputs:

  • Features: $x_1$, $x_2$
  • Parameters: $w_1$, $w_2$, $b$

Forward computation steps:

Step 1: z = w₁x₁ + w₂x₂ + b
        ↓
Step 2: a = σ(z)
        ↓
Step 3: L(a,y) = loss

This is called forward propagation - computing from inputs to loss.

Backward Propagation (Computing Derivatives)

Now we go backwards through the computation graph to compute derivatives.

Step 1: Derivative with respect to $a$

Compute: $\frac{d\mathcal{L}}{da}$ (code variable: da)

\[\frac{d\mathcal{L}}{da} = -\frac{y}{a} + \frac{1-y}{1-a}\]

Note: If you don’t know calculus, that’s okay! We provide all derivative formulas you need.

Step 2: Derivative with respect to $z$

Compute: $\frac{d\mathcal{L}}{dz}$ (code variable: dz)

\[\frac{d\mathcal{L}}{dz} = a - y\]

For calculus experts: This uses the chain rule:

\[\frac{d\mathcal{L}}{dz} = \frac{d\mathcal{L}}{da} \cdot \frac{da}{dz}\]

Where:

  • $\frac{da}{dz} = a(1-a)$ (derivative of sigmoid)
  • Multiplying these gives: $a - y$

Key insight: The derivative simplifies beautifully to just $a - y$!

Step 3: Derivatives with respect to parameters

Compute: $\frac{d\mathcal{L}}{dw_1}$, $\frac{d\mathcal{L}}{dw_2}$, $\frac{d\mathcal{L}}{db}$

\[\frac{d\mathcal{L}}{dw_1} = x_1 \cdot dz\] \[\frac{d\mathcal{L}}{dw_2} = x_2 \cdot dz\] \[\frac{d\mathcal{L}}{db} = dz\]

Code variables: dw1, dw2, db

Summary of Derivatives for One Example

VariableDerivative FormulaCode Variable
$a$$-\frac{y}{a} + \frac{1-y}{1-a}$da
$z$$a - y$dz
$w_1$$x_1 \cdot (a - y)$dw1
$w_2$$x_2 \cdot (a - y)$dw2
$b$$a - y$db

Gradient Descent Update (One Example)

Step 1: Compute derivatives

# Forward pass (already done)
z = w1*x1 + w2*x2 + b
a = sigmoid(z)
loss = -(y*log(a) + (1-y)*log(1-a))

# Backward pass
dz = a - y
dw1 = x1 * dz
dw2 = x2 * dz
db = dz

Step 2: Update parameters

w1 = w1 - alpha * dw1
w2 = w2 - alpha * dw2
b = b - alpha * db

Where $\alpha$ is the learning rate.

Generalizing to $n$ Features

For $n$ features $(x_1, x_2, \ldots, x_n)$:

\[z = \sum_{i=1}^{n} w_i x_i + b = w^T x + b\]

Derivatives:

\[\frac{d\mathcal{L}}{dw_i} = x_i \cdot dz = x_i \cdot (a - y)\]

In vectorized form:

\[\frac{d\mathcal{L}}{dw} = x \cdot dz\]

The Big Picture

Forward propagation (compute loss):

x → z → a → L

Backward propagation (compute gradients):

x ← dz ← da ← dL

Update parameters:

w = w - α · dw
b = b - α · db

What About Multiple Training Examples?

So far, we’ve shown gradient descent for one training example. But in practice, we have $m$ training examples.

Next step: Learn how to apply these concepts to an entire training set efficiently.

Key Takeaways

  1. Forward propagation: Compute predictions and loss
  2. Backward propagation: Compute derivatives using the chain rule
  3. Key formula: $dz = a - y$ (prediction error)
  4. Update rule: Subtract learning rate times gradient
  5. Computation graph: Visual tool for understanding derivatives

Don’t worry about calculus: We provide all the derivative formulas you need. Focus on understanding the flow and implementing the updates correctly.