Last modified: Jan 31 2026 at 10:09 PM • 2 mins read

Logistic Regression

Table of contents

  1. Introduction
  2. Model Parameters
  3. Why Not Use Linear Regression?
  4. The Sigmoid Function
  5. Learning Objective
  6. Next Steps

Introduction

Logistic regression is a learning algorithm for binary classification problems where output labels $y$ are either 0 or 1.

Goal: Given an input feature vector $x$ (e.g., an image), output a prediction $\hat{y}$ that estimates $y$.

Formal Definition: \(\hat{y} = P(y=1 \mid x)\)

This represents the probability that $y = 1$ given the input features $x$.

Example: For a cat image classifier, $\hat{y}$ tells us the probability that the image contains a cat.

Model Parameters

Logistic regression has two sets of parameters:

  • $w$: an $n_x$-dimensional weight vector
  • $b$: a real number (bias term)

Question: Given input $x$ and parameters $w$ and $b$, how do we generate the output $\hat{y}$?

Why Not Use Linear Regression?

Linear Approach (Doesn’t Work)

You might try: \(\hat{y} = w^T x + b\)

Problem with this approach:

  • $\hat{y}$ should be a probability between 0 and 1
  • $w^T x + b$ can be any real number (greater than 1 or even negative)
  • Negative probabilities don’t make sense

This is why linear regression isn’t suitable for binary classification.

The Sigmoid Function

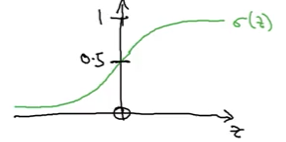
Sigmoid function graph showing an S-shaped curve on an x-y coordinate plane. The y-axis is labeled 1 at the top and 0.5 at the middle. The curve starts near 0 for negative x values, passes through 0.5 at x=0 (marked with a circled plus sign), and asymptotically approaches 1 for positive x values. The function is labeled as sigma of z on the right side of the curve. The curve demonstrates the smooth transition from 0 to 1 that characterizes the sigmoid function used in logistic regression.

Instead, logistic regression uses the sigmoid function to ensure output is between 0 and 1:

\[\hat{y} = \sigma(w^T x + b)\]

Where: \(z = w^T x + b\)

Sigmoid Formula

\[\sigma(z) = \frac{1}{1 + e^{-z}}\]

Sigmoid Properties

Visual behavior:

  • Smoothly increases from 0 to 1
  • Crosses 0.5 at $z = 0$
  • S-shaped curve

Mathematical analysis:

When $z$ is very large (positive):

  • $e^{-z} \approx 0$
  • $\sigma(z) \approx \frac{1}{1 + 0} = 1$

When $z$ is very small (large negative):

  • $e^{-z}$ becomes very large
  • $\sigma(z) \approx \frac{1}{1 + \text{huge number}} \approx 0$

Learning Objective

Your job when implementing logistic regression is to:

Learn parameters $w$ and $b$ such that $\hat{y}$ becomes a good estimate of the probability that $y = 1$.

Next Steps

Now that you understand the logistic regression model, the next step is to define a cost function to learn parameters $w$ and $b$.