Last modified: Jan 31 2026 at 10:09 PM • 6 mins read

What is a Neural Network?

Table of contents

  1. Introduction
  2. Housing Price Prediction Example
  3. The Simplest Neural Network
  4. Building Larger Networks
  5. A More Complex Example: Multi-Feature Housing Prediction
  6. How Neural Networks Actually Work: Dense Connections
  7. Supervised Learning

Introduction

Deep Learning refers to training neural networks, sometimes very large ones. But what exactly is a neural network? Let’s build intuition through a simple example.

Housing Price Prediction Example

The Problem

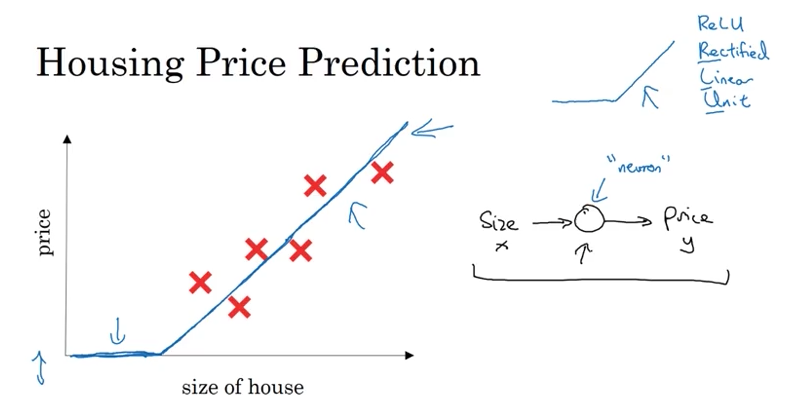
Housing Price Prediction

Suppose you have a dataset with six houses. For each house, you know:

  • Size (in square feet or square meters)
  • Price

You want to fit a function to predict house price based on size.

Simple Linear Regression

If you’re familiar with linear regression, you might fit a straight line to the data. However, there’s a problem: a straight line will eventually predict negative prices, which doesn’t make sense in the real world.

A Better Approach

Since prices can never be negative, we can modify our function:

  • Start at zero when size is zero
  • Then follow a straight line for positive sizes

This creates a function that looks like the thick blue line in the image above. Mathematically, this is:

\[\text{price} = \max(0, w \cdot \text{size} + b)\]

This is actually a very simple neural network! In fact, it’s almost the simplest possible neural network.

The Simplest Neural Network

Structure

  • Input: Size of house ($x$)
  • Neuron: A single processing unit (the circle)
  • Output: Predicted price ($y$)
\[size (x) → [neuron] → price (y)\]

How It Works

The neuron performs these steps:

  1. Takes the input (size)
  2. Computes a linear function: $w \cdot x + b$
  3. Applies $\max(0, \text{result})$ to ensure non-negative output
  4. Outputs the estimated price

The ReLU Function

This $\max(0, z)$ operation is called the ReLU function (Rectified Linear Unit):

\[\text{ReLU}(z) = \max(0, z) = \begin{cases} 0 & \text{if } z < 0 \\ z & \text{if } z \geq 0 \end{cases}\]

The term “rectified” simply means “taking the max with 0,” which creates the bent line shape you see in the graph.

Building Larger Networks

The Lego Analogy

Think of a single neuron as a Lego brick. A larger neural network is built by:

  • Taking many of these single neurons
  • Stacking them together in layers
  • Connecting them in various configurations

Just as you can build complex structures from simple Lego bricks, you can build powerful neural networks from simple neurons.

Key Takeaway

  • Single neuron = Simplest neural network (one input → one output)
  • Deep neural network = Many neurons stacked in multiple layers
  • Each neuron applies a simple transformation, but together they can learn complex patterns

A More Complex Example: Multi-Feature Housing Prediction

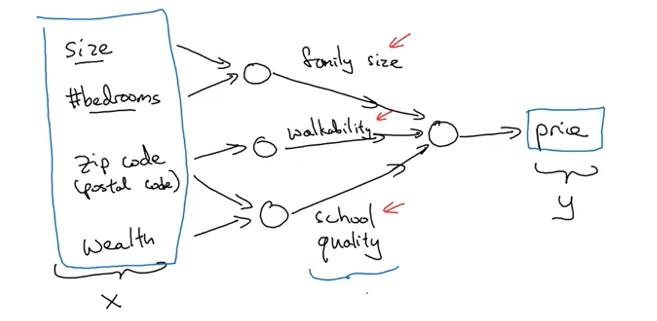
Hand-drawn neural network diagram showing input features on the left in a scroll-like box labeled X with four attributes: size, number of bedrooms, zip code or postal code, and wealth. Arrows point from these inputs to three circular nodes in the middle layer representing neurons labeled family size, walkability, and school quality. These middle neurons have arrows converging to a final circular node on the right connected to a box labeled price with variable y. The diagram illustrates a simple feed-forward neural network architecture with an input layer, hidden layer with three neurons, and output layer predicting housing prices.

Let’s extend our example beyond just using house size. Now we have multiple input features:

Input Features ($x$)

  1. Size (square feet or square meters)
  2. Number of bedrooms (#bedrooms)
  3. Zip code (or postal code)
  4. Wealth (neighborhood affluence level)

Hidden Layer: Derived Features

Instead of directly predicting price, the neural network first computes intermediate features that matter to buyers:

Neuron 1: Family Size Estimation

  • Inputs: Size + Number of bedrooms
  • Purpose: Can this house fit a family of 3, 4, or 5?
  • Logic: Larger homes with more bedrooms accommodate bigger families

Neuron 2: Walkability Score

  • Inputs: Zip code
  • Purpose: How walkable is the neighborhood?
  • Considers:
    • Walking distance to grocery stores
    • Walking distance to schools
    • Need for a car vs. pedestrian-friendly

Neuron 3: School Quality

  • Inputs: Zip code + Wealth
  • Purpose: Quality of local schools
  • Logic: In many countries (especially the US), zip code and neighborhood wealth correlate with school quality

Output Layer: Price Prediction

The final neuron combines these derived features:

  • Inputs: Family size compatibility + Walkability + School quality
  • Output: Predicted price ($y$)
  • Reasoning: People pay based on what matters to them

Network Structure

\[\begin{aligned} \text{Input Layer} &: [size, \text{#bedrooms}, \text{zip code}, \text{wealth}] \\ \text{Hidden Layer} &: [family\_size, walkability, school\_quality] \\ \text{Output Layer} &: [price] \end{aligned}\]

The Magic of Neural Networks

Here’s what makes neural networks powerful:

What you provide:

  • Input ($x$): The four features (size, bedrooms, zip code, wealth)
  • Output ($y$): The actual price (from your training data)

What the network learns automatically:

  • How to combine inputs to estimate family size
  • How zip code relates to walkability
  • How zip code and wealth predict school quality
  • How much weight to give each factor in the final price

You don’t need to explicitly tell the network “compute family size from these inputs” or “calculate walkability.” The network figures out these intermediate representations on its own during training!

Key Insight

By stacking simple neurons together:

  • Each neuron (circle) applies a simple transformation (like ReLU)
  • The hidden layer automatically learns useful intermediate features
  • The network discovers which features matter for prediction
  • All you need to provide is input-output pairs; the network learns the rest

How Neural Networks Actually Work: Dense Connections

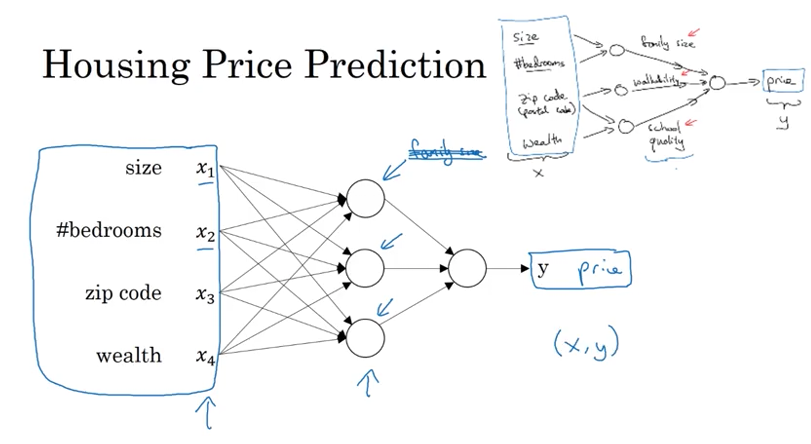
Neural network architecture diagram illustrating densely connected layers

The Real Implementation

In practice, here’s what you actually implement:

Input Layer (4 features):

  • $x_1$: Size
  • $x_2$: Number of bedrooms
  • $x_3$: Zip code
  • $x_4$: Wealth

Hidden Layer (3 neurons):

  • Each neuron receives all 4 input features
  • Not just selected inputs as shown conceptually above

Output Layer:

  • Predicts price $y$

Dense (Fully Connected) Layers

The key difference from our conceptual diagram:

Conceptual view (for intuition):

  • Neuron 1 uses only size + bedrooms → family size
  • Neuron 2 uses only zip code → walkability
  • Neuron 3 uses only zip code + wealth → school quality

Actual implementation:

  • Every neuron receives all 4 inputs
  • The network decides what each neuron should compute
  • We don’t manually specify “neuron 1 = family size”

This is called a densely connected or fully connected layer because:

  • Every input connects to every hidden neuron
  • The network learns which inputs matter for each neuron

Why This Matters

Instead of hard-coding feature relationships, we say:

“Neural network, here are all the inputs. You figure out what each hidden neuron should represent to best predict the price.”

The network automatically learns:

  • Which inputs are relevant for each neuron
  • How to combine those inputs
  • What intermediate features are useful

The Remarkable Property

Given enough training data (many examples of $x$ and $y$), neural networks are exceptionally good at:

  • Finding patterns in the data
  • Learning complex functions
  • Accurately mapping inputs $x$ to outputs $y$

You don’t need to manually design features or specify relationships—the network discovers them through learning!

Supervised Learning

Neural networks are most powerful in supervised learning scenarios:

Definition: Learning a mapping from input $x$ to output $y$ using labeled training examples.

Our example:

  • Input ($x$): House features (size, bedrooms, zip, wealth)
  • Output ($y$): House price
  • Goal: Learn $f(x) = y$

The network sees many (input, output) pairs and learns to predict $y$ from $x$ with high accuracy.