Last modified: Jan 31 2026 at 10:09 PM • 3 mins read

Why Regularization Reduces Overfitting?

Table of contents

  1. Introduction
  2. Problem: Understanding Regularization’s Effect
  3. Intuition 1: Network Simplification Through Weight Reduction
  4. Intuition 2: Linear Activation Regime
  5. Implementation Considerations
  6. Key Takeaways

Neural network diagram comparing overfitting without regularization versus balanced generalization with regularization. Left side shows a complex network with many bright connections labeled High Complexity High Variance producing an erratic wavy red line on a graph labeled WITHOUT REGULARIZATION Overfitting. Center shows a large orange lambda symbol on a balance scale. Right side shows a simpler network with fewer connections labeled Reduced Complexity Better Generalization producing a smooth blue curve labeled WITH REGULARIZATION Balanced. Bottom section shows two mechanisms: 1. NETWORK SIMPLIFICATION - complex network arrows pointing to simple network with text Large Weights Penalized leads to Simpler Model, and 2. LINEAR REGIME - graph showing g of z approximately equals z with text Small Weights leads to Linear Activation leads to Less Complex. Footer text reads Key Concepts: Weight Decay, Bias-Variance Tradeoff, Linearization on dark blue technical background with circuit patterns

Introduction

Regularization is a crucial technique for preventing overfitting in neural networks. This lesson explores the intuitive reasons why regularization works and provides two key perspectives on how it reduces model complexity.

Problem: Understanding Regularization’s Effect

When we add regularization to our cost function, we modify it from:

\[J(W,b) = \frac{1}{m} \sum_{i=1}^{m} \mathcal{L}(y^{(i)}, \hat{y}^{(i)})\]

to:

\[J(W,b) = \frac{1}{m} \sum_{i=1}^{m} \mathcal{L}(y^{(i)}, \hat{y}^{(i)}) + \frac{\lambda}{2m} \sum_{l=1}^{L} \|W^{[l]}\|_F^2\]

The question is: Why does penalizing large weights reduce overfitting?

Intuition 1: Network Simplification Through Weight Reduction

The Mechanism

When we set the regularization parameter $\lambda$ to be very large:

  1. Weight Penalization: The cost function heavily penalizes large weights
  2. Weight Shrinkage: Weights $W^{[l]}$ are driven toward zero
  3. Hidden Unit Impact: Many hidden units have greatly reduced influence
  4. Effective Simplification: The network behaves like a much smaller, simpler model

Mathematical Perspective

For large $\lambda$:

  • Weights approach zero: $W^{[l]} \to 0$
  • Hidden unit activations become negligible
  • Complex network → Simple linear-like model

Bias-Variance Trade-off

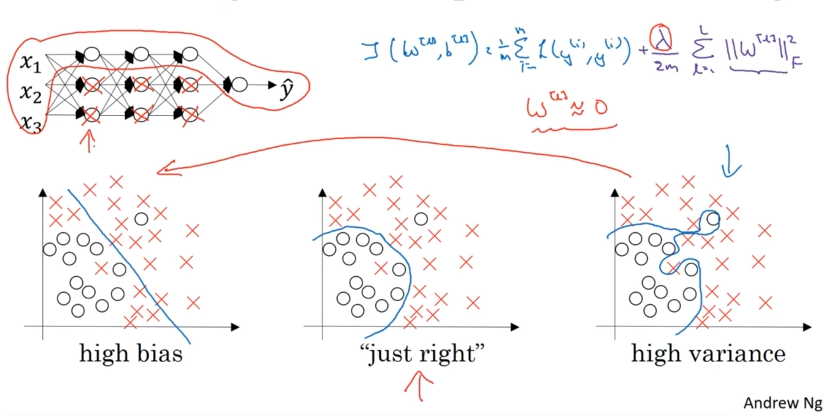
Three scatter plots showing bias-variance tradeoff with circles representing class 0 and X marks representing class 1. Left plot labeled high bias shows underfitting with a linear decision boundary missing most X marks in upper right. Center plot labeled just right shows optimal fit with curved boundary separating classes well. Right plot labeled high variance shows overfitting with irregular boundary wrapping tightly around training points. Above the plots is a neural network diagram with input nodes x1 x2 x3, two hidden layers with interconnected neurons marked with X symbols indicating dropout, and output node y. Arrow points from network to plots. Mathematical notation in corner shows cost function J with weights W and bias b terms plus L2 regularization term with lambda and Frobenius norm, and notation W approximately equals 0. Caption reads Andrew Ng.

Regularization LevelNetwork ComplexityBiasVarianceResult
$\lambda = 0$High complexityLowHighOverfitting
$\lambda$ very largeLow complexityHighLowUnderfitting
$\lambda$ optimalModerate complexityModerateModerateGood fit

Important Clarification

Note: In practice, regularization doesn’t completely zero out hidden units. Instead, it reduces their individual impact while keeping all units active, resulting in a smoother, less complex function.

Intuition 2: Linear Activation Regime

Activation Function Analysis

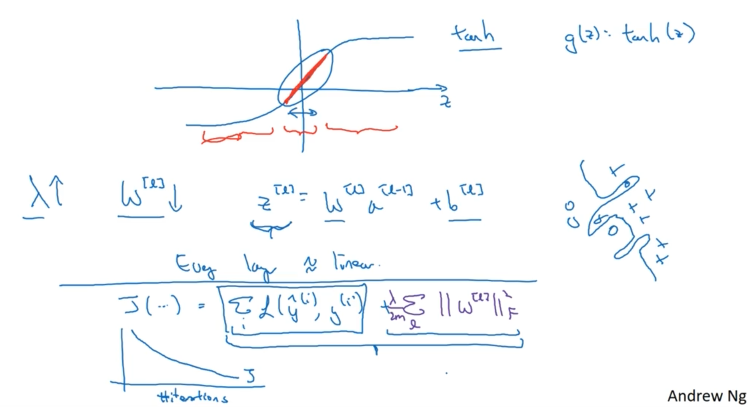
Graph showing tanh activation function with blue S-shaped curve crossing through origin. Horizontal axis labeled z, vertical axis unlabeled. Red oval highlights the central linear region near zero where the curve is approximately straight. Mathematical notation shows g of z equals tanh of z in top right. Handwritten notes below show symbols for lambda pointing up, W pointing down, and equations z squared equals W over a times a plus b squared in brackets. Additional note states Ew log z linear. Expression J of dot equals complex regularization formula with Frobenius norm of W. Small sketch of coordinate axes and curved surface in bottom right. Graph of J decreasing curve versus iterations shown in bottom left. Attribution reads Andrew Ng in bottom right corner.

Consider the $\tanh$ activation function:

\[g(z) = \tanh(z)\]

Key observation: When $z$ is small, $\tanh(z) \approx z$ (linear regime)

How Regularization Creates Linearity

  1. Weight Reduction: Large $\lambda$ → Small weights $W^{[l]}$
  2. Small Linear Combinations: $z^{[l]} = W^{[l]}a^{[l-1]} + b^{[l]}$ becomes small
  3. Linear Activation: When $|z^{[l]}|$ is small, $g(z^{[l]}) \approx z^{[l]}$
  4. Network Linearization: Each layer becomes approximately linear

Mathematical Chain

\[\text{Large } \lambda \to \text{Small } W^{[l]} \to \text{Small } z^{[l]} \to \text{Linear } g(z^{[l]}) \to \text{Linear Network}\]

Why Linear Networks Can’t Overfit

  • Limited Expressiveness: Linear functions can only create linear decision boundaries
  • Reduced Capacity: Cannot fit complex, highly non-linear patterns
  • Overfitting Prevention: Unable to memorize training data noise

Implementation Considerations

Debugging Gradient Descent with Regularization

When implementing regularization, remember to monitor the complete cost function:

# Correct: Include regularization term
J_total = J_loss + (lambda_reg / (2 * m)) * regularization_term

# Monitor J_total for monotonic decrease
plt.plot(iterations, J_total_history)

Warning: If you only plot the original loss term $J_{loss}$, you might not see monotonic decrease during training.

Cost Function Components

ComponentFormulaPurpose
Loss Term$\frac{1}{m} \sum_{i=1}^{m} \mathcal{L}(y^{(i)}, \hat{y}^{(i)})$Fit training data
Regularization Term$\frac{\lambda}{2m} \sum_{l=1}^{L} |W^{[l]}|_F^2$Prevent overfitting
Total CostLoss + RegularizationBalance fit and complexity

Key Takeaways

  1. Weight Shrinkage: Regularization reduces weight magnitudes, simplifying the network
  2. Activation Linearization: Small weights keep activations in linear regime, reducing complexity
  3. Bias-Variance Balance: Proper $\lambda$ selection balances underfitting and overfitting
  4. Implementation: Always monitor the complete regularized cost function during training
  5. Practical Impact: L2 regularization is one of the most commonly used techniques in deep learning