Last modified: Jan 31 2026 at 10:09 PM • 5 mins read

Understanding Dropout

Table of contents

1. Introduction
2. Why Dropout Works: Two Key Intuitions
3. Dropout as Adaptive L2 Regularization
4. Layer-Specific Dropout Rates
5. Hyperparameter Tuning Trade-offs
6. When to Use Dropout
7. Implementation Gotchas
8. Key Takeaways

---

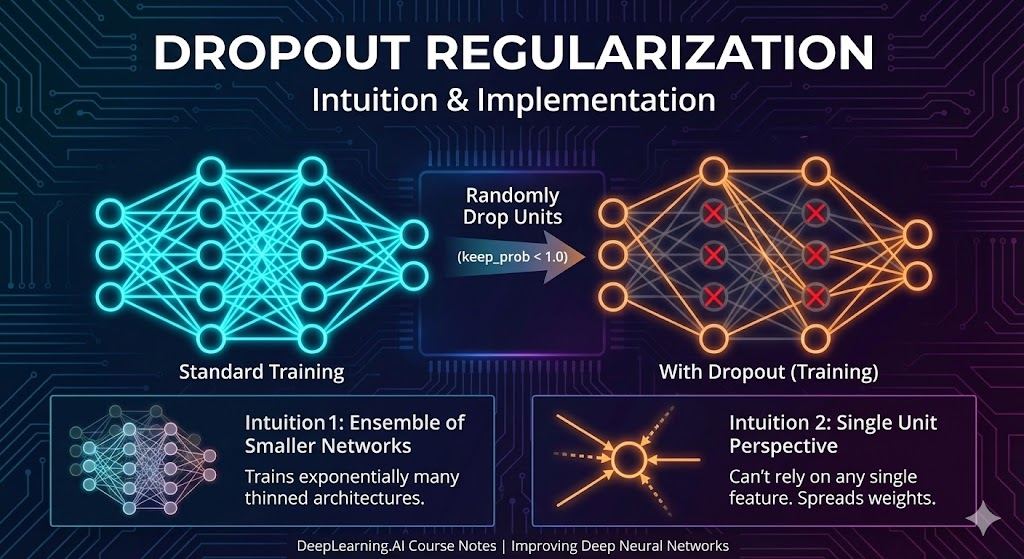
Introduction

Dropout randomly eliminates neurons during training—but why does this seemingly counterintuitive technique work so effectively as a regularizer? Let’s explore the intuitions behind dropout’s success.

Why Dropout Works: Two Key Intuitions

Intuition 1: Training with Smaller Networks

The Effect: Dropout randomly knocks out units in your network on each iteration, forcing the network to work with a smaller, “thinned” architecture.

Why It Helps: Training with smaller neural networks has a natural regularizing effect—smaller networks have less capacity to memorize training data and are forced to learn more generalizable patterns.

Intuition 2: Preventing Feature Co-Adaptation

Let’s examine dropout from the perspective of a single neuron:

The Problem Without Dropout:

• A neuron with 4 inputs might learn to rely heavily on just one or two features
• This creates fragile, specialized connections that don’t generalize well

How Dropout Solves This:

1. Random Input Elimination: Any input to this neuron can be randomly eliminated during training
2. Forced Redundancy: The neuron cannot rely on any single feature because that feature might disappear
3. Weight Spreading: The neuron is motivated to distribute its weights more evenly across all inputs
4. Regularization Effect: Spreading weights reduces the squared norm of weights, similar to L2 regularization

Key Insight: Dropout prevents neurons from co-adapting too much on specific features, forcing them to learn more robust representations.

Dropout as Adaptive L2 Regularization

Dropout can be formally shown to be an adaptive form of L2 regularization, with some important differences:

Aspect	L2 Regularization	Dropout
Weight Penalty	Uniform across all weights	Adaptive based on activation magnitude
Mechanism	Penalize large weights directly	Force weight spreading indirectly
Adaptivity	Fixed λ parameter	Adapts to scale of different inputs

The key difference: Dropout’s L2-like penalty varies depending on the size of the activations being multiplied by each weight, making it more adaptive to the data.

Layer-Specific Dropout Rates

Different layers can use different keep_prob values based on their tendency to overfit.

Choosing Keep_Prob by Layer Size

Consider a network architecture: Input (3) → Hidden1 (7) → Hidden2 (7) → Hidden3 (3) → Hidden4 (2) → Output (1)

Weight Matrix Sizes:

• $W^{[1]}$: 7×3 (21 parameters)
• $W^{[2]}$: 7×7 (49 parameters) ← Largest matrix, most prone to overfitting
• $W^{[3]}$: 3×7 (21 parameters)
• $W^{[4]}$: 2×3 (6 parameters)
• $W^{[5]}$: 1×2 (2 parameters)

Recommended Keep_Prob Values:

keep_prob_1 = 1.0    # Layer 1: Small matrix, no dropout needed
keep_prob_2 = 0.5    # Layer 2: Largest matrix (7×7), aggressive dropout
keep_prob_3 = 0.7    # Layer 3: Medium matrix, moderate dropout
keep_prob_4 = 0.7    # Layer 4: Small matrix, light dropout
keep_prob_output = 1.0  # Output: No dropout

General Guidelines

Layers with MORE parameters → LOWER keep_prob (stronger dropout)

• More parameters = more capacity to overfit
• Apply dropout more aggressively

Layers with FEWER parameters → HIGHER keep_prob (weaker or no dropout)

• Less capacity to overfit
• May not need dropout at all

Input and Output Layer Considerations

Input Layer:

• keep_prob = 1.0 (most common) - no dropout
• Or keep_prob = 0.9 (rarely) - very light dropout
• Reasoning: You rarely want to eliminate input features randomly

Output Layer:

• keep_prob = 1.0 - never use dropout
• Reasoning: You need deterministic outputs for predictions

Hyperparameter Tuning Trade-offs

Option 1: Layer-Specific Keep_Prob

# Different keep_prob for each layer
keep_prob = [1.0, 0.5, 0.7, 0.7, 1.0]

Pros: Maximum flexibility, can optimize each layer individually Cons: More hyperparameters to tune via cross-validation

Option 2: Selective Layer Dropout

# Dropout only on specific layers
keep_prob_layer2 = 0.5  # Only apply to layer 2
# All other layers: no dropout

Pros: Fewer hyperparameters (just one keep_prob) Cons: Less fine-grained control

Think of it like L2 regularization: Just as you can adjust λ to control regularization strength, you adjust keep_prob to control dropout strength per layer.

When to Use Dropout

Computer Vision: Almost Always

Why:

• Input sizes are huge (thousands of pixels)
• Almost never have enough data
• Overfitting is nearly guaranteed
• Computer vision researchers use dropout as default

Other Domains: Only When Overfitting

Rule: Dropout is a regularization technique—only use it if you’re actually overfitting.

Signs You Need Dropout:

• Training accuracy » validation accuracy
• Model performs well on training set but poorly on test set
• Large, complex network with limited data

Signs You Don’t Need Dropout:

• Training and validation accuracy are similar
• You have abundant data
• Model is relatively simple

Important: Don’t use dropout by default—use it as a tool to combat overfitting when needed.

Implementation Gotchas

Downside: Cost Function Monitoring

Problem: The cost function $J$ is no longer well-defined during training with dropout.

Why:

• You’re randomly eliminating neurons on each iteration
• The network architecture changes every iteration
• Hard to verify that $J$ is monotonically decreasing

Solution - Two-Phase Debugging:

# Phase 1: Debug without dropout
keep_prob = 1.0  # Turn off dropout
# Train and verify J decreases monotonically
# Plot cost function to ensure gradient descent works

# Phase 2: Train with dropout
keep_prob = 0.5  # Turn on dropout
# Hope no bugs were introduced
# Monitor validation performance instead of J

Best Practice:

1. First, get your code working without dropout
2. Verify cost function decreases properly
3. Then add dropout and monitor validation metrics
4. Use other debugging methods (validation accuracy, test performance) instead of plotting $J$

Key Takeaways

1. Two Intuitions: Dropout works by training smaller networks and preventing feature co-adaptation
2. Adaptive Regularization: Acts like adaptive L2 regularization based on activation scales
3. Layer-Specific Rates: Use lower keep_prob (stronger dropout) for layers with more parameters
4. Input/Output: Typically no dropout on input (keep_prob ≈ 1.0) and never on output
5. Domain-Specific: Common in computer vision (always overfitting), less common elsewhere
6. Use When Needed: Only apply dropout if you’re actually overfitting
7. Debugging Challenge: Cost function monitoring is harder—debug without dropout first
8. Hyperparameter Tuning: Balance between layer-specific flexibility and simplicity