Last modified: Jan 31 2026 at 10:09 PM • 5 mins read

Dropout Regularization

Table of contents

  1. Introduction
  2. The Dropout Concept
  3. Implementing Inverted Dropout
  4. Understanding Inverted Dropout Scaling
  5. Training vs. Test Time
  6. Dropout Variations Across Layers
  7. Implementation Best Practices
  8. Comparison: Dropout vs. L2 Regularization
  9. Key Takeaways

Neural network architecture comparison showing a fully connected network on the left with 4 input features (x1, x2, x3, x4) connected through multiple hidden layers to output y-hat, versus the same network on the right with dropout applied where several neurons marked with red X symbols have been randomly eliminated along with their connections, demonstrating how dropout creates a thinned network structure during training. The image includes code snippets showing the inverted dropout implementation with d3 = np.random.rand(...) < keep_prob, a3 *= d3, and a3 /= keep_prob for training time, and z3 = np.dot(W3, a2) + b3, a3 = np.tanh(z3) with no scaling for testing time. A magnifying glass highlights the dropped neurons in purple and blue tones against a dark background, with the title Dropout Regularization Inverted Implementation: Training vs. Testing at the top.

Introduction

Dropout is a powerful regularization technique that randomly “drops out” (eliminates) neurons during training. Unlike L2 regularization which penalizes large weights, dropout creates an ensemble effect by training many different “thinned” versions of the network.

The Dropout Concept

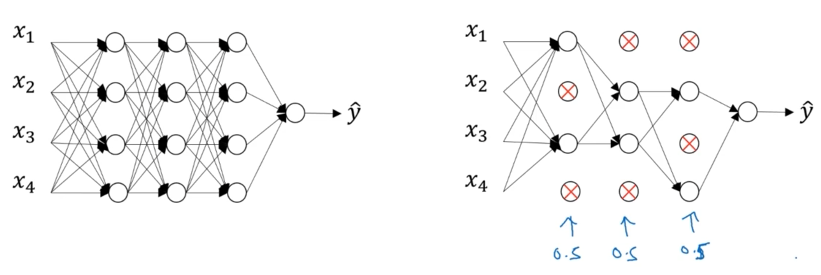
Neural network architecture comparison showing a fully connected network on the left with 4 input features (x1, x2, x3, x4) connected through multiple hidden layers to output y-hat, versus the same network on the right with dropout applied where several neurons marked with red X symbols have been randomly eliminated along with their connections, demonstrating how dropout creates a thinned network structure during training

How Dropout Works

For each training iteration:

  1. Random Selection: For each layer, randomly eliminate neurons with probability $(1 - \text{keep_prob})$
  2. Network Reduction: Remove selected neurons and all their connections
  3. Train Reduced Network: Perform forward and backpropagation on this smaller network
  4. Repeat: For each training example, randomly drop different neurons

Visualization

StageDescription
Full NetworkComplete neural network before dropout
Apply DropoutRandomly eliminate 50% of neurons (if keep_prob = 0.5)
Reduced NetworkTrain on smaller “thinned” network
Next IterationDifferent random neurons dropped

Key Insight: Each training example sees a different “architecture,” preventing neurons from relying too heavily on specific other neurons (co-adaptation).

Implementing Inverted Dropout

The Standard Implementation

Inverted dropout is the most common and recommended implementation. It handles scaling during training rather than at test time.

Step-by-Step Implementation for Layer 3

Step 1: Create Dropout Mask

# Generate random dropout mask
d3 = np.random.rand(a3.shape[0], a3.shape[1])  # Same shape as a3
d3 = (d3 < keep_prob)  # Boolean mask: True = keep, False = drop

Step 2: Apply Mask to Activations

# Zero out dropped neurons
a3 = a3 * d3  # Element-wise multiplication
# Or equivalently: a3 *= d3

Step 3: Scale Up (Inverted Dropout)

# Scale activations to maintain expected value
a3 = a3 / keep_prob
# Or equivalently: a3 /= keep_prob

Complete Code Example

# Training with inverted dropout for layer 3
keep_prob = 0.8  # Keep 80% of neurons, drop 20%

# Forward propagation
z3 = np.dot(W3, a2) + b3
a3 = np.tanh(z3)  # Or any activation function

# Apply dropout
d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep_prob
a3 *= d3          # Zero out dropped neurons
a3 /= keep_prob   # Scale up remaining neurons

# Continue with next layer
z4 = np.dot(W4, a3) + b4
# ...

Understanding Inverted Dropout Scaling

Why Scale by keep_prob?

Consider a layer with 50 neurons and $\text{keep_prob} = 0.8$:

Without Scaling:

  • On average, 20% of neurons (10 units) are zeroed out
  • Expected value: $E[a^{[3]}] = 0.8 \times a^{[3]}_{\text{original}}$
  • Next layer receives 20% less input than expected
  • Problem: $z^{[4]} = W^{[4]}a^{[3]} + b^{[4]}$ is reduced by 20%

With Inverted Dropout Scaling:

\[a^{[3]} = \frac{a^{[3]} \odot d^{[3]}}{\text{keep_prob}}\]
  • Dividing by 0.8 compensates for the 20% reduction
  • Expected value preserved: $E[a^{[3]}] = a^{[3]}_{\text{original}}$
  • No scaling needed at test time

Mathematical Justification

\[E[a^{[3]}_{\text{scaled}}] = E\left[\frac{a^{[3]} \odot d^{[3]}}{\text{keep_prob}}\right] = \frac{\text{keep_prob} \cdot a^{[3]}}{\text{keep_prob}} = a^{[3]}\]

Training vs. Test Time

During Training

# Apply dropout on every forward pass
for iteration in range(num_iterations):
    # Different random dropout mask each iteration
    d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep_prob
    a3 *= d3
    a3 /= keep_prob
    
    # Backpropagation also uses the same mask
    da3 *= d3
    da3 /= keep_prob

Important: Use a different random dropout mask for:

  • Each training example
  • Each pass through the training set
  • Each layer (with potentially different keep_prob values)

During Testing

# NO dropout at test time
z1 = np.dot(W1, a0) + b1
a1 = g1(z1)

z2 = np.dot(W2, a1) + b2
a2 = g2(z2)

z3 = np.dot(W3, a2) + b3
a3 = g3(z3)
# ... and so on

# Make prediction without randomness
y_pred = a_L

Critical: Never apply dropout during prediction/testing. You want deterministic outputs, not random ones.

Why No Dropout at Test Time?

ApproachProsCons
Dropout at testEnsemble averagingComputationally expensive, random outputs
No dropout (inverted)Fast, deterministicRequires proper training-time scaling ✓

Inverted dropout advantage: Because we scaled during training, test time requires no modifications—just use all neurons with their learned weights.

Dropout Variations Across Layers

Different layers can have different keep_prob values:

# Layer-specific dropout rates
keep_prob_1 = 1.0   # Input layer: no dropout
keep_prob_2 = 0.9   # First hidden: 10% dropout
keep_prob_3 = 0.5   # Second hidden: 50% dropout (prone to overfitting)
keep_prob_4 = 0.8   # Third hidden: 20% dropout
keep_prob_output = 1.0  # Output layer: no dropout

Rule of thumb: Apply stronger dropout (lower keep_prob) to layers with more parameters or those prone to overfitting.

Implementation Best Practices

Key Points

  1. Use inverted dropout: Industry standard, simplifies test time
  2. Different masks per iteration: Ensures true randomness
  3. No dropout at test time: Use full network for predictions
  4. Layer-specific rates: Adjust keep_prob based on layer size and overfitting risk
  5. No dropout for input/output: Usually keep these layers intact

Common Mistakes to Avoid

❌ Wrong: Same dropout mask for all training examples ❌ Wrong: Applying dropout at test time ❌ Wrong: Forgetting to scale by keep_prob (non-inverted dropout) ❌ Wrong: Using dropout when no overfitting exists

✅ Correct: Random mask per iteration + inverted scaling + no test-time dropout

Comparison: Dropout vs. L2 Regularization

AspectDropoutL2 Regularization
MechanismRandomly eliminate neuronsPenalize large weights
ImplementationModify forward/backward passAdd term to cost function
ComputationSlightly faster (fewer neurons)Full network always used
Test TimeNo modification needed (inverted)No modification needed
Tuning Parameterkeep_prob per layerSingle $\lambda$
Best ForLarge networks, computer visionAny network, interpretable

Key Takeaways

  1. Ensemble Effect: Dropout trains many “thinned” networks, creating ensemble-like behavior
  2. Inverted Dropout: Scale during training ($a /= \text{keep_prob}$) to avoid test-time scaling
  3. Random Per Iteration: Use different dropout masks for each training example
  4. No Test-Time Dropout: Use full network with all neurons for predictions
  5. Expected Value Preservation: Inverted dropout maintains activation scale across train/test
  6. Layer-Specific Rates: Adjust keep_prob based on overfitting tendency per layer
  7. Industry Standard: Inverted dropout is the recommended implementation