Last modified: Jan 31 2026 at 10:09 PM • 7 mins read

Bias / Variance

Table of contents

1. Introduction
2. Visual Intuition: The Three Classifiers
3. Diagnosing Bias and Variance with Error Metrics
4. Four Classic Scenarios
5. Decision Framework
6. High Bias + High Variance: How Is This Possible?
7. The Role of Bayes Error
8. Summary: Two-Step Diagnostic Process
9. Important Caveats
10. Key Takeaways

---

Introduction

Understanding bias and variance is a critical skill that separates good machine learning practitioners from great ones. While the concepts are easy to learn, they’re surprisingly difficult to master - there are nuances that reveal themselves only with experience.

The Deep Learning Era Shift

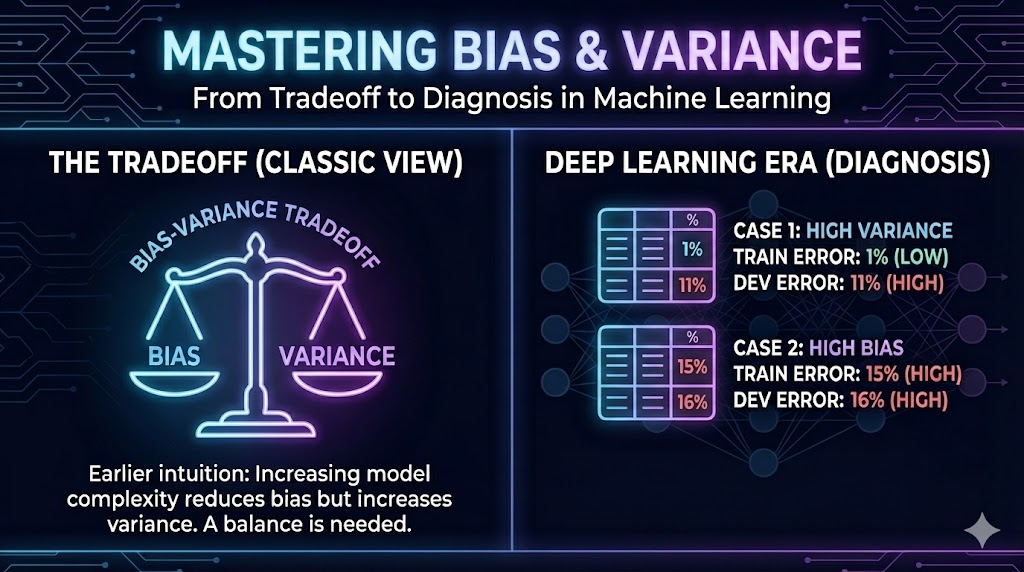
In traditional machine learning, people often discussed the “bias-variance tradeoff” - the idea that reducing bias increases variance and vice versa. However, in the deep learning era:

We still talk about bias and variance, but the tradeoff has become less restrictive.

With modern techniques (more data, regularization, bigger networks), we can often reduce bias without increasing variance, or reduce variance without increasing bias. Let’s explore how to diagnose and fix these issues.

Visual Intuition: The Three Classifiers

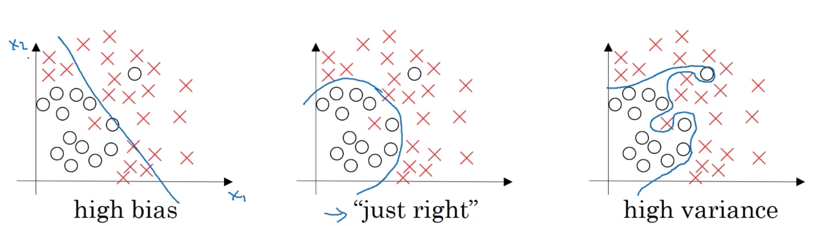
2D Classification Example

Consider a binary classification problem with features $x_1$ and $x_2$:

Characteristics:

Classifier Type	Complexity	Fits Training Data	Generalizes Well	Problem
High Bias	Too simple (e.g., linear)	❌ No	N/A	Underfitting
Just Right	Appropriate	✅ Yes	✅ Yes	None
High Variance	Too complex	✅ Yes	❌ No	Overfitting

The Challenge in High Dimensions

In 2D, you can visualize the decision boundary and see bias/variance issues directly. But in high-dimensional problems (e.g., cat classification with millions of pixels), you can’t plot the data.

Solution: Use quantitative metrics instead of visual inspection.

Diagnosing Bias and Variance with Error Metrics

The Two Key Numbers

To diagnose bias and variance, compare these errors:

1. Training set error: How well does your model fit the training data?
2. Dev set error: How well does your model generalize to new data?

Assumptions for This Analysis

Important: This analysis assumes that human-level performance (or Bayes error) is nearly 0%.

For tasks like recognizing cats in clear photos, humans achieve ~0% error. We’ll discuss more complex cases later.

Four Classic Scenarios

Scenario 1: High Variance

Metric	Value	Interpretation
Training error	1%	Excellent fit to training data
Dev error	11%	Poor generalization
Diagnosis	High Variance	Overfitting

Analysis:

• Model performs well on training set (1% error)
• Performance degrades significantly on dev set (11% error)
• Gap of 10% indicates the model memorized training data rather than learning general patterns

Visual analogy: This is like the rightmost plot - the complex, wiggly decision boundary.

Scenario 2: High Bias

Metric	Value	Interpretation
Training error	15%	Poor fit even to training data
Dev error	16%	Slightly worse on dev set
Diagnosis	High Bias	Underfitting

Analysis:

• Model can’t even fit the training set well (15% error)
• Dev set performance is only slightly worse (16% error)
• Small gap (1%) means model is consistently underperforming
• Model is too simple to capture underlying patterns

Visual analogy: This is like the leftmost plot - the straight line that doesn’t fit the data.

Scenario 3: High Bias AND High Variance (Worst Case!)

Metric	Value	Interpretation
Training error	15%	Poor fit to training data
Dev error	30%	Much worse on dev set
Diagnosis	High Bias + High Variance	Worst of both worlds

Analysis:

• Model doesn’t fit training data well (15% error) → High bias
• Model generalizes even worse (30% error) → High variance
• This happens when the model is wrong in multiple ways

How is this possible? See the next section for explanation.

Scenario 4: Low Bias AND Low Variance (Ideal!)

Metric	Value	Interpretation
Training error	0.5%	Excellent fit to training data
Dev error	1%	Excellent generalization
Diagnosis	Low Bias + Low Variance	Optimal performance

Analysis:

• Model fits training data nearly perfectly (0.5% error)
• Model generalizes well (1% error)
• Small gap (0.5%) indicates good generalization
• This is your goal!

Decision Framework

Here’s a quick decision tree for diagnosis:

\[\begin{align} \text{Training error high?} &\implies \text{High Bias (Underfitting)} \\ \text{Dev error ≫ Training error?} &\implies \text{High Variance (Overfitting)} \\ \text{Both conditions true?} &\implies \text{High Bias + High Variance} \\ \text{Both conditions false?} &\implies \text{Low Bias + Low Variance (Good!)} \end{align}\]

Concrete Thresholds (Cat Classification Example)

Assuming human-level performance ≈ 0%:

Training Error	Dev Error	Dev - Train Gap	Diagnosis
< 2%	< 3%	< 1%	✅ Low bias, low variance
< 2%	> 5%	> 3%	⚠️ Low bias, high variance
> 5%	Similar to train	< 1%	⚠️ High bias, low variance
> 5%	Much higher	> 5%	🚫 High bias, high variance

High Bias + High Variance: How Is This Possible?

2D Example (Appears Contrived)

Imagine a classifier that is:

• Mostly linear (underfits most of the data) → High bias
• Extremely flexible in some regions (overfits noise/outliers) → High variance

Characteristics:

• Linear portion underfits the quadratic shape (high bias)
• Small wiggles overfit individual noisy examples (high variance)
• Needs a smooth quadratic curve, not a linear function with bumps

Why This Matters in High Dimensions

While this 2D example might seem contrived, in high-dimensional problems this is quite common:

Example: Image classification

• Model might be too simple for certain features (underfitting face detection) → High bias
• Model might be too complex for other features (overfitting background patterns) → High variance
• Different parts of the input space can have different bias/variance characteristics

In neural networks:

• Early layers might underfit (high bias)
• Later layers might overfit (high variance)
• Different neurons can specialize in different ways

The Role of Bayes Error

What is Bayes Error?

Bayes error (or optimal error) is the best possible error rate achievable by any classifier, even with infinite data. It represents irreducible error due to:

• Label noise (mislabeled examples)
• Overlapping classes (impossible to distinguish)
• Information loss (insufficient features)
• Inherent randomness

When Bayes Error Affects Your Analysis

Standard assumption: Bayes error ≈ 0% (humans can perform the task perfectly)

But what if the task is inherently difficult?

Example: Blurry image classification

If images are so blurry that even humans can only achieve 15% accuracy:

Metric	Value	Standard Analysis	Corrected Analysis
Bayes error	15%	(Assumed 0%)	(Actual)
Training error	15%	High bias?	Actually optimal!
Dev error	16%	High bias?	Low bias, low variance

Key insight: Compare your errors to Bayes error, not to 0%.

Practical Implications

When Bayes error is significant:

\[\text{Bias} = \text{Training error} - \text{Bayes error}\] \[\text{Variance} = \text{Dev error} - \text{Training error}\]

Example with Bayes error = 15%:

Training error: 15%, Dev error: 16%

• Bias = 15% - 15% = 0% (low bias!)
• Variance = 16% - 15% = 1% (low variance!)

We’ll cover this in more detail in later lessons on human-level performance.

Summary: Two-Step Diagnostic Process

Step 1: Check Training Error (Measures Bias)

\[\text{Training error vs Bayes error} \implies \text{Bias assessment}\]

• Training error close to Bayes error: Low bias ✅
• Training error much higher than Bayes error: High bias ⚠️

Step 2: Check Dev Error Gap (Measures Variance)

\[\text{Dev error vs Training error} \implies \text{Variance assessment}\]

• Small gap (< 1-2%): Low variance ✅
• Large gap (≫ 2%): High variance ⚠️

Combined Diagnosis Table

Train Error	Dev - Train Gap	Diagnosis	Action Needed
Low	Low	✅ Good model	Deploy!
Low	High	🟡 High variance	More data, regularization
High	Low	🟡 High bias	Bigger model, more features
High	High	🔴 Both problems	Address bias first

Important Caveats

This analysis assumes:

1. ✅ Bayes error is small (task is feasible)
2. ✅ Train and dev sets drawn from same distribution (no distribution shift)

If either assumption is violated, you need more sophisticated analysis (covered in later lessons).

Key Takeaways

1. Critical skill: All great ML practitioners deeply understand bias and variance
2. Two metrics: Training error and dev error tell you everything you need
3. High bias (underfitting): Model too simple, can’t fit training data well
4. High variance (overfitting): Model too complex, doesn’t generalize to dev set
5. Both possible: High-dimensional models can have high bias AND high variance
6. Training error: Measures how well you fit the data (bias indicator)
7. Dev-train gap: Measures how well you generalize (variance indicator)
8. Bayes error matters: Compare to optimal error, not always 0%
9. Blurry images: When task is inherently hard, Bayes error is high
10. Distribution assumption: Train and dev must be from same distribution
11. No more tradeoff: Deep learning can reduce both bias and variance
12. Visual intuition: Linear = high bias, wiggly = high variance, smooth curve = just right
13. High-dim complexity: Bias/variance can vary across different input regions
14. Diagnostic first: Always diagnose before trying to fix